هندسة الصف الاول الثانوي الفصل الدراسي الاول
التشابه
1)تشابه المضلعات
2)تشابه المثلثات
3)العلاقة بين مساحتي مضلعين متشابهين
4)العلاقة بين مساحتي مثلثين متشابهين
التشابه
1)تشابه المضلعات
تقال لمضلعين لهما نفس العدد من الاضلاع انهما متشابهان إذا تحقق الشرطان الآتيان معا :-
1-تساوي قياسات الزوايا المتناظرة
2-تناسب اطوال الاضلاع المتناظرة
اهم الملاحظات :-
1. يفضل عند كتابة المضلعين المتشابهين ان نكتبهما بنفس ترتيب رءوسهما المتناظرة
2. اذا تشابه مضلعان فإن
|-تتساوي قياسات الزوايا المتناظرة
||-تتناسب اطوال الاضلاع المتناظرة
4.المضلعات المنتظمة التي لها نفس العدد من الاضلاع تكون متشابهه
2)تشابه المثلثات
هناك 3 حلات لتشابه مثلثين :-
- إذا طابقت زاويتان في مثلث زاويتان في مثلث آخر فانهما متشابهان
- إذا تناسبت أطوال الأضلاع المتناظرة في مثلثين فإنهما يتشابهان
- إذا طابقت زاوية في مثلث زاوية في مثلث آخر و تناسبت أطوال الأضلاع التي تحتويها هاتين الزاويتين فإنهما يتشابهان
3)العلاقة بين مساحتي مضلعين متشابهين
النسبة بين مساحتي مضلعين متشابهين تساوي مربع النسبة بين طولي ضلعين متناظرين فيهما
4)العلاقة بين مساحتي مثلثين متشابهين
النسبة بين مساحتي مثلثين متشابهين تساوي مربع النسبة بين طولي ضلعين متناظرين فيهما
@النسبة بين محيطي مضلعين متشابهين تساوي النسبة بين طولي ضلعين متناظرين فيهما
@النسبة بين محيطي مثلثين متشابهين تساوي النسبة بين طولي ضلعين متناظرين فيهما
@ النسبة بين مساحتي مثلثين مشتركين ( متساويين) في الارتفاع تساوي النسبة بين طولي قاعدتيهما المناظرتين لهذيىن الارتفاعين
@ النسبة بين مساحتي مثلثين مشتركين ( متساويين) في القاعدة تساوي النسبة بين ارتفاعيهما المناظرين لهاتين القاعدتين
@يتشابه المثلثان القائما الزاوية إذا ساوي قياس زاوية حادة في احدهما قياس زاوية حادة في الآخر
@يتشابه المثلثان المتساويا الساقين إذا ساوي قياس زاوية في احدهما قياس زاوية مناظرة لها في الآخر
@ المضلعات المنتظمة التي لها نفس العدد من الاضلاع تكون متشابهة
@ كل المثلثات المتساوية الأضلاع متشابهه
@ كل الاشكال الخماسية المنتظمة متشابهه
@ كل الاشكال السداسية المنتظمة متشابهه
@ كل الاشكال السباعية المنتظمة متشابهه ... و هكذا
@اذا رسم مستقيم يوازي احد اضلاع مثلث ويقطع الضلعين الاخرين فانه يقسمهما الي قطع اطوالها متناسبة.
نظريات التناسب فى الهندسة
نظرية (1)
إذا رسم مستقيم يوازى أحد أضلاع المثلث ويقطع الضلعين الآخرين فإنه يقسمهما الى قطع أطوالهامتناسبة
(2) إذا كانت أطوال القطع الناتجة على أحد القاطعين متساوية فى الطول فإن أطوال القطع الناتجة على أى قاطع آخر تكون متساوية فى الطول
ملاحظات فى هامة
(1) المنصفان الداخلى والخارجى لزاوية فى مثلث يقسمان القاعدة من الداخل ومن الخارج بنفس النسبة بين طولى الضلعين الاخرين للمثلث
(2) المنصفان الداخلى والخارجى لزاوية فى مثلث يكونان متعامدان
(3) منصف الزاوية الداخلة عند راس المثلث المتساوى الساقين ينصف القاعدة
(4) منصف الزاوية الخارجة عند راس المثلث المتساوى الساقين يوازى القاعدة
هذا الراس حسب حالة التقسيم
التشابه : - تشابه مضلعين : - يقال لمضلعين(لهما نفس عدد الاضلاع)
انهما متشابهان :إذاتحقق الشرطين الاتيين معا : -
(1)تساوى قياساتالزوايا المتناظرة (2)تناسب اطوال الاضلاع المتناظرة
ملاحظات هامة
(1)يجب كتابة المضلعين بنفس ترتيب رءوسهما المتناظرة
(2) إذاتشابه مضلعان فإننا نستنتج أن : - (1) قياسات زواياهما المتناظرة متساوية
(2)أطوال أضلاعهما المتناظرة متناسبة
(3)المضلعان المتطابقان متشابهان بينما ليس من الضرورى ان يكون المضلعان المتشابهان متطابقين
(4)المضلعان المشابهان لثالث متشابهان
(5) اى مضلعين منتظمين لهما نفس عدد الاضلاع يكونان متشابهين
تشابه المثلثات :- الحالة الاولى ـــ نظرية 4
إذا ساوت قياسات زوايا أحد مثلثين قياسات نظائرهما فى المثلث الاخر كان المثلثان متشابهان
ملاحظات
(1)يتشابه المثلثان إذاساوى قياسا زاويتين من احدهما قياسا زاويتين فى الاخر
(2) يتشابه المثلثان القائما الزاوية إذاساوىقياس زاوية حادة من احدهما إذاساوى قياس زاوية حادة من الاخر
(3) يتشابه المثلثان المتساويا الساقين إذاساوىقياس إحدى زاويتى القاعدة فى احدهما قياس إحدى زاويتى القاعدة فى الاخر
(4) إذا رسم مستقيم يوازى احد اضلاع مثلث ويقطع الضلعين الاخرين او امتداد يهما فان المثلث الناتج
عكس نظرية (1)
إذا قطع مستقيم ضلعين من أضلاع مثلث وقسمهما الى قطع أطوالها متناسبة فإنه يوازى الضلع الثالثنظرية (2) ( تاليس العامة )
إذا قطع مستقيمان عدة مستقيمات متوازية فإن أطوال القطع الناتجة على أحد القاطعين تكون متناسبة مع أطوال القطع الناتجة على القاطع الآخر.حالة خاصة :
(2) إذا كانت أطوال القطع الناتجة على أحد القاطعين متساوية فى الطول فإن أطوال القطع الناتجة على أى قاطع آخر تكون متساوية فى الطول
نظرية (3)
إذا نصفت زاوية راس مثلث أو الزاوية الخارجة عند هذا الراس قسم المنصف قاعدة المثلث من الداخل او من الحارج الى جزاين النسبة بين طوليهما كالنسبة بين طولى الضلعين الاخرين للمثلثملاحظات فى هامة
(1) المنصفان الداخلى والخارجى لزاوية فى مثلث يقسمان القاعدة من الداخل ومن الخارج بنفس النسبة بين طولى الضلعين الاخرين للمثلث
(2) المنصفان الداخلى والخارجى لزاوية فى مثلث يكونان متعامدان
(3) منصف الزاوية الداخلة عند راس المثلث المتساوى الساقين ينصف القاعدة
(4) منصف الزاوية الخارجة عند راس المثلث المتساوى الساقين يوازى القاعدة
عكس نظرية (3)
إذا قسمت نقطة احد اضلاع مثلث من الداخل او من الخارج الى جزاين النسبة بين طوليهما تساوى النسبة بين طولى الضلعين الاخرين كان الشعاع الذى مبدؤه الراس المقابل مارا بنقطة التقسيم هو المنصف للزاوية الداخلة او الخارجة عندهذا الراس حسب حالة التقسيم
التشابه : - تشابه مضلعين : - يقال لمضلعين(لهما نفس عدد الاضلاع)
انهما متشابهان :إذاتحقق الشرطين الاتيين معا : -
(1)تساوى قياساتالزوايا المتناظرة (2)تناسب اطوال الاضلاع المتناظرة
ملاحظات هامة
(1)يجب كتابة المضلعين بنفس ترتيب رءوسهما المتناظرة
(2) إذاتشابه مضلعان فإننا نستنتج أن : - (1) قياسات زواياهما المتناظرة متساوية
(2)أطوال أضلاعهما المتناظرة متناسبة
(3)المضلعان المتطابقان متشابهان بينما ليس من الضرورى ان يكون المضلعان المتشابهان متطابقين
(4)المضلعان المشابهان لثالث متشابهان
(5) اى مضلعين منتظمين لهما نفس عدد الاضلاع يكونان متشابهين
تشابه المثلثات :- الحالة الاولى ـــ نظرية 4
إذا ساوت قياسات زوايا أحد مثلثين قياسات نظائرهما فى المثلث الاخر كان المثلثان متشابهان
ملاحظات
(1)يتشابه المثلثان إذاساوى قياسا زاويتين من احدهما قياسا زاويتين فى الاخر
(2) يتشابه المثلثان القائما الزاوية إذاساوىقياس زاوية حادة من احدهما إذاساوى قياس زاوية حادة من الاخر
(3) يتشابه المثلثان المتساويا الساقين إذاساوىقياس إحدى زاويتى القاعدة فى احدهما قياس إحدى زاويتى القاعدة فى الاخر
(4) إذا رسم مستقيم يوازى احد اضلاع مثلث ويقطع الضلعين الاخرين او امتداد يهما فان المثلث الناتج
تذكر أن : -
(1)الزاوية المحيطية المرسومة فى نصف دائرة قائمة وقياسها = 90 درجة(2)الزوايا المحيطية التى تحصر نفس القوس فى الدائرة او اقواس متساوية او فى دوائر متطابقة متساوية
(3)قياس الزاوية المماسية يساوى قياس الزاوية المحيطية المرسومة على وتر التماس من الجهة الاخرى
(4)فى الشكل الرباعى الدائرى كل زاويتين متقابلتين متكاملتان
(5)قياس الزاوية الخارجة عند اى راس من رؤوس شكل رباعى دائرى = المقابلة للمجاورة لها
نتيجة هامة
إذارسم من راس القائمة فى المثلث القائم الزاوية عمود على الوتر انقسم المثلث الى مثلثين متشابهين وكل منهما يشابه المثلث الاصلىالحالة الثانية نظرية(5)
إذاساوى قياس زاوية من مثلث قياس زاوية من مثلث اخر وتناسبت اطوال الاضلاع التى تحتويها هاتان الزاويتان فإن المثلثين يتشابهان
الحالة الثالثة نظرية (6)
إذاتناسبت أطوال الاضلاع المتناظرة فى مثلثين فإن المثلثين يتشابهان
نظرية(7)
النسبة بين مساحتى مثلثين متشابهين تساوى مربع النسبة بين اى ضلعين متناظرين
ملاحظة :-
النسبة بين محيطى مثلثين متشابهين تساوى النسبة بين اى ضلعين متناظرين فيهما اى نسبة التكبير
ملاحظات
حقيقة هندسية
المضلعان المتشابهان يمكن ان ينقسما الى نفس العدد من المثلثات التى يشابه كل منها نظيرةنظرية( 5)
النسبة بين مساحتى مضلعين متشابهين تساوى مربع النسبة بين طولى اى ضلعين متناظرين فيهما
ملاخظة النسبة بين محيطى مضلعين متشابهين بتساوى النسبة بين اى ضلعين متناظرين بدون التربيع
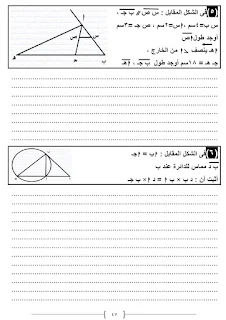
فإن م أ × م ب = م جـ × م د
وكان م أ× م ب= م جـ × م د
ملاخظة النسبة بين محيطى مضلعين متشابهين بتساوى النسبة بين اى ضلعين متناظرين بدون التربيع
تمارين مشهورة
(1) إذاتقاطع المستقيمان الحاويان للوترين أ ب , جـ د لدائرة داخلها او خارجها فى نقطة م حيث م ليست مركز الدائرةفإن م أ × م ب = م جـ × م د
عكس التمرين المشهورالسابق
إذاتقاطع المستقيمان الحاويان للقطعتين أب , جـ د فى نقطة م ( مختلفة عن أ , ب , جـ , د)وكان م أ× م ب= م جـ × م د
فإن النقط أ , ب , جـ , د تقع على دائرة
ويكون الشكل الرباعى دائرى
, م ب يقطعها فى أ , ب فإن
نتيجة هامة
إذاكانت م نقطة خارج دائرة , م جـ يمس الدائرة عند جـ, م ب يقطعها فى أ , ب فإن
( م جـ )^2= م أ × م ب
و كل النظري و تمارين شيقه في مذكرة المميز للاستاذ الكبير / ياسر علي جزاه الله خيرا
معاينة الملف من هناااااااا
مذكرةالهندسة للصف الأول الثانوي الترم الأول ملف PDF من هنااااااااااااااا
لو عاوز :
مذكرةالجبر للصف الأول الثانوي الترم الأول ملف PDF من هنااااااااااااااا
مراجعة تطبيقات الرياضيات (سؤال و جواب)الصف الثاني الثانوي الفصل الدراسى الاول من هناااااااااااااااااااااااا
تحميل كل كتب وزارة التربية و التعليم كل السنوات من من الرابط من هناااااااااااااااااا
تحميل تطبيق مدرستنا للأندرويد
أطلقت وزارة التربية والتعليم قناة مدرستنا التعليمية في تقديم البرامج التعليمية لطلاب الصفوف الآتية:الصف الرابع الابتدائى
الصف الخامس الابتدائى
الصف السادس الابتدائى
الصف الأول الإعدادي
الصف الثانى الإعدادي
الصف الثالث الإعدادي.