الجبر للصف الأول الثانوي | الفصل الدراسي الاول | مذكرة روووعة شاملة
الدرس الأول : مقدمة عن الاعداد المركبة
💖 ط={0 ، 1 ، 2 ، 3 ، 4 ،.....}
💖 ص={......، -4 ، - 3 ، -2 ، -1 ، 0 ، 1 ، 2 ، 3 ، 4 ،.....}
💖 ح = ن ∪ ن⧵
💖 ن ∩ ن⧵ = ∅
💖 كــــ = {س+ت ص : س ، ص ∈ ح ، ت ^ 2 = -1 }
💖إذا انعدم عدد مركب ينعدم مل من جزأه الحقيقي و التخيلي كل علي حدة
💖 إذا تساوي عددين مركبين تساوي الحقيقي مع الحقيقي و التخيلي مع التخيلي و العكس صحيح
💖ت ^ (4ن) = 1
💖ت ^ (4ن+1) = ت
💖ت ^ (4ن+2 )= -1
💖ت ^ (4ن+3) = - ت
💖(2 + 5 ت)+(-7 + 3 ت)=-5 + 3 ت
💖(2 + 5 ت)-(-7 + 3 ت)=12 + 2 ت
💖(2 + 5 ت)(-7 + 3 ت)=- 29 - 29ت
💖(2 +5ت)/(-7+3ت)=1/ 58-41/ 58ت
💖 مرافق العدد 3 + 5 ت هو 3 -5 ت
💖(3 + 5 ت) +(3 -5 ت )= 2 ×3 = 6
💖(3 + 5 ت) (3 -5 ت )= 9+25 =34
💖|-3 + 4 ت| = (9+16)^0.5=5
💖مرافق مجموع عددين = مجموع مرافقيهما
💖مرافق خارج قسمة عددين = مرافق البسط/مرافق المقام
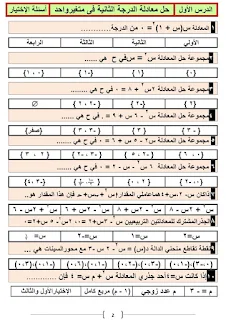
الدرس الثاني : تحديد نوع جذري المعادلة التربيعية
💖 مميز المعادلة : أ س ^2 + ب س + جــ = 0 هو ب^2 - 4 × أ × جــ
💖 إذا كان : المميز > صفر فإن الجذران حقيقيان مختلفان
💖إذا كان : المميز < صفر فإن الجذران مركبان غيرحقيقيان مختلفان
💖إذا كان : المميز = صفر فإن الجذران حقيقيان متساويان
الدرس الثالث : العلاقة بين جذري المعادلة التربيعية و معاملاتها
💖المعادلة : أ س ^2 + ب س + جــ = 0
💖 أ = معامل س^2
💖ب = معامل س
💖جـ = الحد الخالي من س (المطلق)
💖الجذران هما : ل ، م
💖 ل + م = - ب / أ
💖 ل × م = جـ / أ
الدرس الرابع : تكوين المعادلة التربيعية متي علم جذراها
💖 (س-الجذر الأول)(س-الجذر الثاني) = صفر
💖س ^2 - ( ل + م) س + ( ل × م ) = 0
💖ل^2 + م^2 = ( ل + م )^2 - 2 ل م
💖ل^2 × م^2 = ( ل م )^2
💖ل/م + م/ل = (( ل + م )^2 - 2 ل م)/(ل م)
💖1/ل + 1/م = (ل + م)/(ل م)
💖 ( ل - م ) ^ 2 = ( ل + م )^2 - 4 ل م
💖ل^3 + م^3 = ( ل + م )^3 - 3 ل م(ل + م)
💖ل^3 - م^3 = ( ل - م )(( ل + م )^2 - ل م)
💖(ل + ك)(م + ك) = ل م +ك( ل + م ) + ك^2
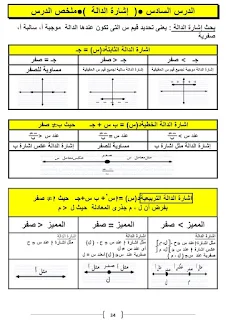
الدرس الخامس : إشارة الدالة (الثابتة و الخطية و التربيعية)
💖الدالة الثابتة : د(س)=أ موجبة إذا كانت أ موجبة و سالبة إذا كانت أ سالبة و ليست موجبة و لا سالبة إذا كانت أ =صفر
💖الدالة الخطية : د(س)=أ+ب س
مثل إشارة ب إذا كانت س > - أ / ب ، عكس إشارة ب إذا كانت س < - أ / ب ، و ليست ليست موجبة و لا سالبة إذا كانت س < - أ / ب
💖الدالة التربيعية : د(س)=أس ^2+ ب س + جــ
* مثل إشارة أ لكل س ∈ ح إذا كان المميز سالبا
*مثل إشارة أ لكل س ∈ ح -{ - ب / (2أ)} إذا كان المميز صفراً و ليست موجبة و لا سالبة إذا كانت : س = - ب / (2أ)
*مثل إشارة أ لكل س ∈ ح -[ل ، م] إذا كان المميزموجباً و عكس إشارة أ لكل س ∈ ]ل ، م[ و ليست موجبة و لا سالبة إذا كانت : س ∈ {ل ، م}
الدرس السادس : متباينات الدرجة الثانية في مجهول واحد
💖 حلها يعتمد علي إشارة الدالة
و كل النظري و تمارين شيقه في مذكرة المميز للاستاذ الكبير / ياسر علي جزاه الله خيرا
معاينة المذكرة
مذكرةالجبرللصف الأول الثانوي الترم الاول ملف PDF من هنااااااااااااااا
مذكرة الهندسةالصف الاول الثانوى الفصل الدراسي الاول من هنااااااااااااا
مراجعة تطبيقات الرياضيات (سؤال و جواب)الصف الثاني الثانوي الفصل الدراسى الاول من هناااااااااااااااااااااااا
تحميل كل كتب وزارة التربية و التعليم كل السنوات من من الرابط من هناااااااااااااااااا
تحميل تطبيق مدرستنا للأندرويد
أطلقت وزارة التربية والتعليم قناة مدرستنا التعليمية في تقديم البرامج التعليمية لطلاب الصفوف الآتية:الصف الرابع الابتدائى
الصف الخامس الابتدائى
الصف السادس الابتدائى
الصف الأول الإعدادي
الصف الثانى الإعدادي
الصف الثالث الإعدادي.